Proof of the Chain Rule
Considering a composite function 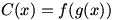 , we write a difference quotient for the derivative: , we write a difference quotient for the derivative: 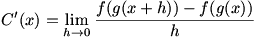 . Now let’s define . Now let’s define 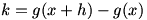 so so 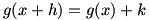 . Then we substitute that into our difference quotient, giving . Then we substitute that into our difference quotient, giving 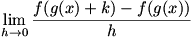 . We multiply both the numerator and denominator by . We multiply both the numerator and denominator by 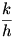 to get to get 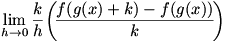 . Clearly . Clearly 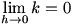 from the definition of from the definition of 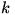 , so we can consider our limit to be a , so we can consider our limit to be a 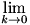 . Now we notice that the second factor in the limit is a difference quotient that gives . Now we notice that the second factor in the limit is a difference quotient that gives 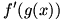 , so we now know that , so we now know that 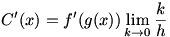 . .
To find the value of 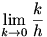 , we use the difference quotient for , we use the difference quotient for 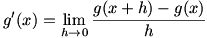 , but the numerator of that is how we defined , but the numerator of that is how we defined 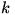 (noting our assumption that (noting our assumption that 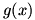 is differentiable). Therefore is differentiable). Therefore  and we have and we have  . This is the chain rule. . This is the chain rule.


| 