Lesson 2.8: Higher-Order Derivatives
Differentiation is an operation that takes in a function and also outputs a function. Of course, it’s mathematically reasonable that we could then put that function back in, differentiating the original function a second time. In fact, this is a common and useful process known as taking the second derivative. Naturally, we can extend this further to taking third derivatives and so forth.
You’ll hopefully recall that we notate the (first) derivative of a function 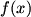 as as 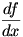 or or 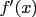 . The first notation can be more explicitly written as . The first notation can be more explicitly written as 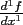 . You will never actually see it written this way, but with that in mind it’s perfectly reasonable that we write a second derivative as . You will never actually see it written this way, but with that in mind it’s perfectly reasonable that we write a second derivative as 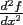 or or 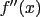 , and so forth. Since large number of prime marks tend to get unwieldy, fourth derivatives in Lagrange’s notation are written , and so forth. Since large number of prime marks tend to get unwieldy, fourth derivatives in Lagrange’s notation are written 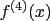 , and so on. , and so on.
This concept can further be extended to 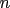 th derivatives, th derivatives, 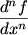 or or 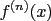 , and a couple of examples will hopefully suffice to make this clear. , and a couple of examples will hopefully suffice to make this clear.
Starting with a function 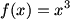 , we already know that , we already know that 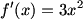 . As we’ve just discovered, we can differentiate again to get . As we’ve just discovered, we can differentiate again to get 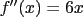 , and perhaps even another time for , and perhaps even another time for 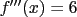 . (We could go on ad infinitum, if we really wanted to, but all higher derivatives are zero.) . (We could go on ad infinitum, if we really wanted to, but all higher derivatives are zero.)
It’s a little more interesting to repeatedly differentiate functions like 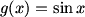 . First we get . First we get
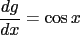 as expected. And if we take the second derivative, we have
as expected. And if we take the second derivative, we have
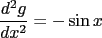 and a third time,
and a third time,
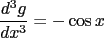 But if we shoot for the moon and take the fourth derivative, we’re back where we started:
But if we shoot for the moon and take the fourth derivative, we’re back where we started:
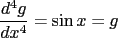
Teachers like to exploit the cyclic nature of this by asking you for such seemingly crazy things as the 53rd derivative of 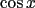 . Rather than work through fifty-three iterations of repetitive hell, you’ll be better off realizing that every fourth derivative is the same as the original. Since . Rather than work through fifty-three iterations of repetitive hell, you’ll be better off realizing that every fourth derivative is the same as the original. Since 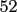 is divisible by is divisible by 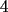 and and 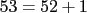 (don’t use your calculator), the 53rd derivative is the same as the first, so (don’t use your calculator), the 53rd derivative is the same as the first, so
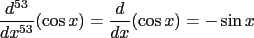
What are higher derivatives good for? We’ll see some uses of them in related rates, and they’re the essence of Taylor series (hang on until April for those). More importantly, though, they’re very common in physics. If you have taken physics, you hopefully will remember that given position 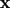 , velocity , velocity 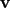 , and acceleration , and acceleration 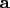 , we can define , we can define 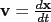 and and 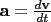 . We can combine these last two to get . We can combine these last two to get
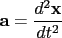 —all of these, you should definitely know. For some real fun,
—all of these, you should definitely know. For some real fun, 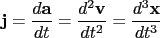 And that’s quite enough for today.
And that’s quite enough for today.


| 