|
About
Lessons
Handouts
Practice
AP Questions
Contact
M&EMs
|
Lesson 1.2: The Limit
From Algebra II, you will remember the informal definition of a limit: if a function 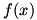 approaches a value L while its input x approaches a value a, we write approaches a value L while its input x approaches a value a, we write 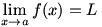 and say “the limit of f of x as x approaches a equals L”. These limits can be finite or infinite, and the function may or may not actually reach the limit. and say “the limit of f of x as x approaches a equals L”. These limits can be finite or infinite, and the function may or may not actually reach the limit.
|
For example, consider 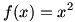 . Then, . Then, 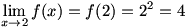 . This may be informally demonstrated by examining the graph of . This may be informally demonstrated by examining the graph of 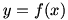 and noting that and noting that 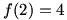 and and 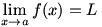 is near 4 whenever x is near 2. is near 4 whenever x is near 2. |
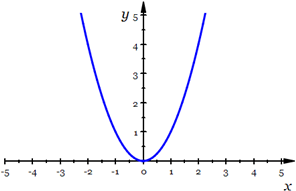
The graph of 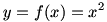 |
|
Things are not always so simple, however. Take 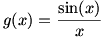 around around 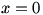 . Because division by zero is not allowed, . Because division by zero is not allowed, 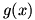 is undefined at is undefined at 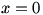 . But if we graph . But if we graph 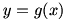 , it appears that , it appears that 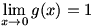 (this is correct, which we will prove later in Chapter 2). Again using our informal definition of a limit, which we will soon make rigorous, it is clear that functions can have a limit where they are undefined. (this is correct, which we will prove later in Chapter 2). Again using our informal definition of a limit, which we will soon make rigorous, it is clear that functions can have a limit where they are undefined.
|
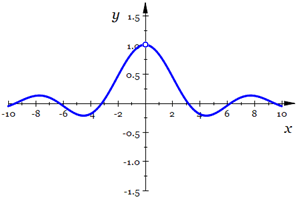
The graph of 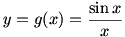 |
|
Now let’s examine 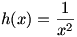 . Again, . Again, 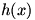 is undefined at is undefined at 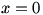 . Looking at the graph of . Looking at the graph of 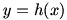 , it seems that , it seems that 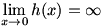 . The limit doesn’t exist, but we often speak of a function having an infinite limit; that is, it gets larger and larger (or negatively so) without bound. . The limit doesn’t exist, but we often speak of a function having an infinite limit; that is, it gets larger and larger (or negatively so) without bound.
|
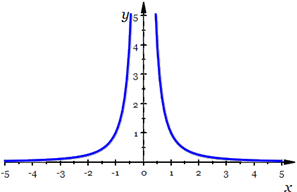
The graph of 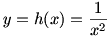 |
|
The final type of limit we need to consider is the one-sided limit. Consider 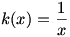 . Once again, . Once again, 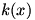 is undefined at is undefined at 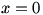 , but if we look at the graph of , but if we look at the graph of 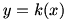 , it would be incorrect to say that , it would be incorrect to say that 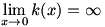 because this is only true if we approach because this is only true if we approach 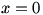 from the positive x-axis. If we take from the positive x-axis. If we take 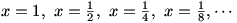 , we can get as large a value of , we can get as large a value of 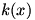 as we like; that is, as we like; that is, 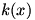 approaches ∞. But if we take approaches ∞. But if we take 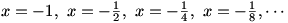 , , 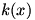 gets infinitely small; that is, it approaches gets infinitely small; that is, it approaches 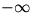 . Since the value of the limit is different depending on which side it is approached from, we write . Since the value of the limit is different depending on which side it is approached from, we write 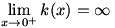 and and 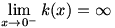 . In general, we say that . In general, we say that 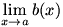 exists if and only if exists if and only if 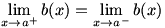 (and both, of course, exist). (and both, of course, exist).
|
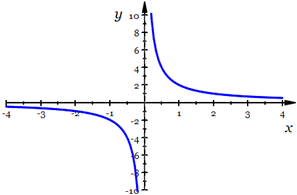
The graph of 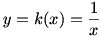 |
|
Occasionally, we find a function 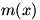 where the limit at a certain value (let’s call it a) of x exists, but where the limit at a certain value (let’s call it a) of x exists, but 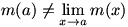 . This is fairly unusual; it most frequently occurs in piecewise-defined functions such as . This is fairly unusual; it most frequently occurs in piecewise-defined functions such as 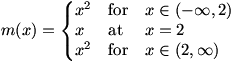 . In this case, . In this case, 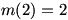 , but as can be seen from the graph of , but as can be seen from the graph of  , , 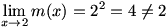 . .
|
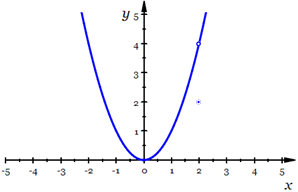
The graph of 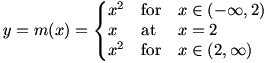 |
After a brief diversion to the discussions of continuity and evaluating limits, we will arrive at a formal definition of a limit. While this intuitive concept of a limit is generally sufficient, the study of mathematics is concerned with rigor. Therefore, we will soon discuss the foundation of calculus: Augustin-Louis Cauchy’s delta-epsilon definition of the limit.


|
